Optimal payment scheme for a Dutch Bank Savings Mortgage, using a Mixed Integer Linear Program

There is a special type of mortgage in the Netherlands (Bank Savings Mortgage or bankspaarhypotheek in Dutch), which I presume, does not exist anywhere else in the world. The construct is that you have a mortgage on your house for a certain amount, say 200000 €, and split it up into two parts:

one part with a loan (in this case 200000), where you pay only interest
a second part which is a savings account.

Usually both of these accounts have the same interest rates and you pay a fixed amount per year so that in the end the savings account can be used to pay off the loan. For the bank, this construct is exactly identical to having just one account with a loan that is paid off like an annuitary mortgage with a fixed amount per month.

The difference is in the way this type of mortgage is taxed. On the loan part, the interest is tax deductable, and the savings account is not taxed at all. Therefore in comparison with an annuitary mortgage, where the loan gets less over time (it is equivalent before taxes), there is more tax deduction. And this is what makes it an attractive type of mortgage.

With this type of mortage it is possible to pay off parts of the loan part or to add extra money to the savings account. When given a choice, adding a given amount to the savings account is a lot more attractive than using it to pay off the mortgage. Even though it is equivalent to the bank, putting it into the savings account leads to a higher tax deduction.

But of course, the government has put forward some rules to prevent people from profiting too much, and these make it challenging to determine an optimal scheme to pay of the mortgage to minimize total payments made. For this purpose, this post examines a simple Mixed Linear Integer Program (MILP).

The rules

To start with, there are rules for how long the mortgage should be run (the banks also don’t make any money if people pay off their mortgage too soon). In addition, there is the infamous bandwidth rule, which states that for each mortgage year, the maximum amount saved in the savings account should be less than 10 times the minimum amount saved in a mortgage year. For instance, if your mortgage started in February, then each mortgage year runs from the start of February of one year to the end of January of the next year.

This bandwidth rule has some interesting implications. Suppose for instance that, initially, you have mandatory payments for the savings account of 200 per month or 2400 per year. Then, in year 2, you pay an additional amount of 10000 which causes the total payment to go to say 12000 (not 12400 since because of the payment, the monthly amount after the payment in the second year goes down immediately). Then in year 3, because of the extra payment, you only pay 1200 per year. Then, in this case the bandwidth limit of 10 ( $=\frac{12000}{1200}$ ) is already reached. As a result of this it is impossible to make any more additional payments into the savings account since that would exceed the bandwidth limit. In this case, it may make more sense to make a lower payment of say 3000 in the second year, and then gradually increase, making sure not to exceed the bandwidth.

In the above example, even without making additional payments, the bandwidth could be also be exceeded if the interest rate on the mortage increases. This is why banks in general enforce a lower bandwidth of say 7 or 8. This makes this mortgage less predictable and a bit risky, except if you fix the interest rate for the entire duration of the mortgage.

As can be seen in the example, it can be quite complex to determine an optimal scheme for additional payments, since there are so many things to consider. Fortunately, this problem can be quite easily formulated as a MILP.

Model variables

First we define a number of variables to model the savings account:

$\left\{ \begin{array}{ll} s_i \ge 0 & \text{The amount at the start of month\ }i \\ v_i \ge 0 & \text{The mandatory payment at the start of month\ } i \\ e_i \ge 0& \text{The additional payment made at month \ } i\\ s_{max}, s_{min} \ge 0 & \text{The minimum, respectively maximum, amount} \\ & \text{saved over all mortgage years} \\ \end{array} \right.$

Here, $i$ is the month number.

In addition, there is a restriction from the bank that when a payment is made, the payment must be at least a given amount (say 500). To model this we need a binary variable that indicates whether or not a payment was made:

$\begin{array}{ll} \delta_i = 0, 1& \text{Indicates whether\ } e_i \ge 0 \\ \end{array}$

In addition we introduce some variables into the model for the costs that are convenient to let the model compute the quantities that we are interested in. Instead of having to compute them ourselves afterwards. These are $c_{fixed}$ , $c_{extra}$ , and $c$ for fixed payments, additional payments, and total payments respectively, where of course $c = c_{fixed} + c_{extra}$ .

Model parameters

We define the following input parameters:

$\left\{ \begin{array}{ll} y_0 & \text{Year that the computation starts} \\ m_0 & \text{Starting month 1-12 of the mortage year} \\ L & \text{The (remaining) mortgage running time in years} \\ r & \text{The monthly interest rate} \\ H & \text{The target mortgage amount}\\ S & \text{The initial amount of the savings account} \\ M & \text{The minimal amount for additional payments} \\ B & \text{Maximum allowed bandwidth} \\ S_{max} & \text{The maximum amount saved so far} \\ S_{min} & \text{The minimum amount saved so far} \end{array} \right.$

Therefore $i = 1, \ldots, 12L$ for $s$ , $v$ , and $e$ . For $s$ the value $i = 12L+1$ is also used since that represents the savings account at the end of the mortgage period.

In the model, we assume that the interest rate is constant, although it is very easy to adapt this to a changing interest rate. Also, because we include the initial amount $S$ and the current minimum and maximum saved amounts $S_{min}$ and $S_{max}$ so far, it is possible to also model a mortgage starting midway.

Model conditions

To start with we have the initial and terminating conditions:

$\left\{ \begin{array}{ll} s_1 = S & \text{initial amount saved} \\ s_{12L+1} = H & \text{completely paid off at the end} \\ s_{max} \ge S_{max} & \text{include earlier payments in bandwidth} \\ s_{min} \le S_{min} & \text{include earlier payments in bandwidth} \\ \end{array} \right.$

In addition, we have to define the history of additional payments in the model. For instance, if a mortgage year starts in February, and it is October now, then the additional payments for February through to September must be included. This involves setting $e_i = 0$ for months without payments and setting $e_i$ to non zero values for those months where additional payments were made.

Next we model that the saving account increases due to interest, fixed payments, and additional payments.

$s_{i+1} = rs_{i} + v_i + e_i$

For each next month the fixed amount is computed by assuming fixed payments as follows

$r^{12L-i+1} s_i + \frac{r^{12L-i+1}-1}{r-1}v_i = H$

The minimum payment is modeled using the $\delta_{i}$ variable:

$M \delta_i \le e_i \le H\delta_i$

Clearly, if $\delta_i = 0$ , then $e_i = 0$ and $e_i \ge M$ otherwise, thereby modeling the minimum payment rule.

Next are the bandwidth requirements. First we define the bandwidth variables:

$s_{min} \le \sum_{i = 12y+1}^{12y+12} (v_i + e_i) \le s_{max} \quad y = 0, \ldots, L-1$

and then we have the bandwidth restriction

$s_{max} \le B s_{min}$

Finally, we define the cost variables:

$\left\{ \begin{array}{l} c_{fixed} = \sum_{i = 1}^L v_i \\ c_{extra} = \sum_{i = 1}^L e_i \\ c = c_{fixed} + c_{extra} \end{array} \right.$

and the minimization problem

$\min c$

Code

The code is written in R and uses the lpSolve package or gurobi if present. The model appears quite easy since both solvers can solve this problem within a fraction of a second.

There are two files:

banksparen.R: which is the file that defines the parameters and the model.
LPModel.R: A R6 utitlity class for defining MILP problems in general. It uses lpSolve or gurobi to solve the MILP problem.

Example

The output from running the model with the example parameters is as follows

> extraPaymentsDf = extraPaymentsDf %>%
+   filter(extraPayment > 0)
> extraPaymentsDf
# A tibble: 4 x 5
   year month extraPayment fixedPaymentBefore fixedPaymentAfter
                                      
1  2019     4         5000                259               223
2  2020     2         5550                223               183
3  2021     2         6099                183               137
4  2022     2         5566                137                93
> 
> 
> extraPaymentsFuture = sum(solution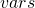e[timeIndex(curYear, curMonth):length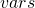(solutione)])
> fixedPaymentsFuture = sum(solution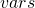v[timeIndex(curYear, curMonth):length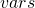(solutione)])
> 
> cat('Total extra payments in the future: ', extraPaymentsFuture, '\n')
Total extra payments in the future:  17215.16 
> cat('Total fixed payments in the future: ', fixedPaymentsFuture, '\n')
Total fixed payments in the future:  21543.87 
> cat('Total payments in the future      : ', solution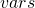costs, '\n')
Total payments in the future      :  45651.6

The output correctly shows the payment that was made in April 2019 and shows three payments to be done at the start of mortgage years 2020, 2021, and 2022 respectively. It also shows the monthly fixed amount before and after the payment. This information is also useful to verify the computation. In my case (different parameter values!), the monthly amounts get within 1 EUR of what I am actually paying. By experimenting with the model, it also becomes easy to see what the effect would be of smaller and larger payments on the total amount paid and on the monthly payments. This makes it a very nice tool to experiment with.

Optimal payment scheme for a Dutch Bank Savings Mortgage, using a Mixed Integer Linear Program

Leave a Reply Cancel reply

Categories

Recent Posts

Recent Comments

Archives

Meta